We use the formula
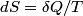 . We assume the system has reached thermal equilibrium. This means that the two bodies must have the same temperature. Conservation of energy implies that this temperature must be . We assume the system has reached thermal equilibrium. This means that the two bodies must have the same temperature. Conservation of energy implies that this temperature must be 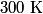 . If the equilibrium temperature were greater than . If the equilibrium temperature were greater than 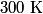 , the amount of heat enters the body originally at , the amount of heat enters the body originally at 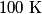 would be greater than the amount of heat that leaves the body originally at would be greater than the amount of heat that leaves the body originally at 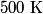 . If the equilibrium temperature were less than 300 K, the amount of heat that leaves the body originally at . If the equilibrium temperature were less than 300 K, the amount of heat that leaves the body originally at 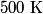 would be greater than the amount of heat that enters the body originally at would be greater than the amount of heat that enters the body originally at 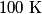 . Both situations violate conservation of energy (this assumes, of course, that the heat capacity . Both situations violate conservation of energy (this assumes, of course, that the heat capacity 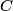 is a constant). The entropy change of the body originally at is a constant). The entropy change of the body originally at 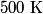 is is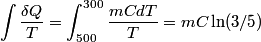 The entropy change of the body originally at 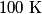 is is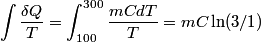 Therefore, the total entropy change is 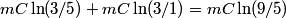 Hence answer (B) is correct. |